The contents of
the first part of this page until the "stereoscopic
ratio" was presented at KAPiCA 2002, the international
conference on kite aerial photography, on November 5th,
2002 and has been updated and completed since.
FOREWORD
The
key of success in photographic stereoscopy
is to have a clear understanding and knowledge
of the stereoscopic process and of the parameters
which control it. We also have observed
that stereoscopy is more or less effective
depending on situations, and we will see
how to deal with it for successful pictures.
This page describes
the fundamentals. |
|
CONDITION
FOR STEREOSCOPY
Stereoscopy is
a physiological and geometric process.
To get a stereoscopic sensation, the image
in our left eye and the image in our right
eye must be similar, but with slight geometric
differences. In this case, our brain will
interpret the scene for stereoscopic effect.
If the two images have no differences, the
stereoscopic effect does't exist.
From
this, it issues that stereoscopy is effective
with the condition that:
|
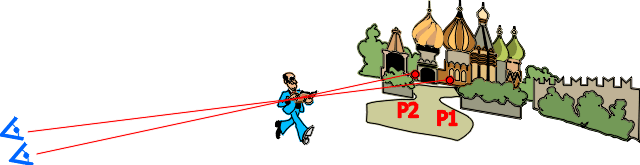
Dots
P1 and P2 must be differentiated by our eyes
PHYSIOLOGICAL
LIMITS

- Keenness of eye
The keenness is
the ability of our eye to make out two close
points. We cannot distinguish two points
which are within an angle less than one
minute. Mathematically, keenness is an angle
expressed in radian unit: a
= 0.0003 to 0.0004
|
|
- Color separation
We can only distinguish
colors if their area is large enough, and
if the surroundings have a different tint.
This may affect considerably the stereoscopic
effect because the left and right image
may not be different.
|
PARAMETERS
OF THE SCENERY
There are one non-geometric
and two geometric parameters to consider
Background
disposition
If the background
is of the same uniform color, there is no
stereoscopic effect. It is the case of a
seagull seen flying in an uniform deep blue
sky. Our eye cannot see any difference between
P1 and P2. If the background
is variegate, with many different colored
and contrasted areas, P1
and P2
are really different, and there will be
stereoscopic effect. The background disposition
is a non-geometric parameter.
-
On a photograph,
there is not only one foreground and only
one background, but a succession of plans,
one of them being the foreground of the
next one, and the background of the one
before.
The formulas can
be calculated for each couple of successive
plans depending on their real arrangement.
|
|
- Distance between
camera and subject
This parameter
will apply as angle between lines L1 and
L2 must be greater than the keenness limit.
As D increases,
the angle decreases.
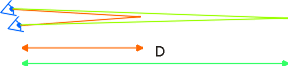
- Distance between
subject and background
The further is
the background behind the subject, the more
P1 and P2 will be distant.
It means that just behind a far subject,
there is an area where stereoscopy is non
effective because the dots P1
and P2 will
not be differentiated. It is named the neutral
zone.

|
PARAMETERS
OF THE OBSERVER
The observer can use his eyes, but
also binoculars, mirror devices, cameras, and so on. All
these are optically different, and will affect stereoscopic
effect. Applied to photography, the camera constituted of
the lens and of the sensor, and the restitution device can
change the stereoscopic rendering.
- The Base
For us the base
is the distance between our eyes, common
value is 63mm. Using cameras, the base can
be modified and it is the only parameter
that we can change for stereoscopic effectiveness
control. The larger is the base, the more
stereoscopy will be effective
|
|
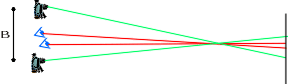
The orthostereoscopy is when the base is
equal to the distance between the eyes. |
RULES
AND GEOMETRIC FORMULAS
-
Let's consider
the distances B,
D, L,
and keenness a,
when applying stereoscopic condition we
have two basic relations:
e/(D+L) > a and
B/D
= e/L
|
-
|
- From these, formulas are easy to get:
Non effective
zone N
= a . D² / (B - a . D)
-
Base B > a
. D (D+L) / L
|
STEREOSCOPIC
RATIO

The base formula
will give the minimum base to use. As we
said, the stereoscopic sensation can be
strong or weak. So, it is interesting for
us to appreciate and scale this stereoscopic
sensation, at least from the geometric parameters.
For this, we will use the stereoscopic ratio
SR
I must admit that I don't know any
universal recognized rule or formula for
this purpose. For years, I applied the formula
that I published in Aerial Eye summer 1998,
which I draw from a book.
But I observed
that it was not working properly in some
cases even it was satisfactory in most cases.
After unsuccessful researches in a few books
I went on my own, reconsidered the
whole thing, expressed a new line of argument,
and set a polyvalent formula.
Note: The formulas are set for
a stereoscopic angle of view identical to
the human vision which doesn't exceed 60°
|
-
|
The minimum space
of two dots that the eye can see on the
background is s,
and the gap of projected points of the subject
on the background is e:
let's compare it as angles: e/(D+L) and
s/'D+L) or e/s.
The Stereoscopic
Ratio is SR =
e / s
If e=s Stereoscopic
Ratio is 1
- With e = B L/D
and s = a (D+L) we
obtain:
SR = B L / a D (D+L)
- Tables can be calculated. For
the human eye:
- 0
< SR < 1 no stereoscopic
effect.
1
< SR < 10 weak stereoscopic
effect
10<
SR < 20 moderate stereoscopic
effect
20
< SR < 35 heightened stereoscopic
effect
35
< SR < 50 strong stereoscopic
effect
50
< SR < 70 excessive stereoscopic
effect
- further the
stereoscopy is disturbing or impossible.
|
LIMITS of
STEREOSCOPIC EFFECT
Maximum Stereoscopic
Ratio:
Start from the
formula: SR = B L /
a D (D+L)
and
define t = L/D
we
get SR = B/ (a.D) .
t / (1+t)
It can be verified
that 0
< t/(1+t) <1 which gives the formula
of the maximum stereoscopic ratio.
Mathematical considerations
lean to:
SR
max = B / (a . D)
which
occurs when the background is at infinity
and which varies decreasing with the distance
to the field.
|
|
Maximum
stereoscopic distance of the eye:
The maximum stereoscopic
effect is got when the background is at
infinity. Let's find the maximum distance
of a field to which the stereoscopic effect
becomes imperceptible to the human eye.
In this case, SR = 1
The before formula
is then written D = B / a
The space of eyes
is 63mm,
Dmax
= 0.063 / 0.0004 = 157 m
Behind
this distance, everything is a neutral zone.
|
Neutral zone:
Already mentionned,
the neutral zone is where there is no stereoscopic
effect. It can be defined two ways:
¤ Zone for
which the field behind the subject is too
close.
¤ Zone further
than D max
Physically, in
both cases, for the eye, it is the zone
where the stereoscopic ratio is inferior
to 1. Thus SR<1 is also e<s.
.The extent
of neutral zone behind the subject is
calculated by :
N
= SR .
a
.
D²
/ (B - a . D)
The distance
behind which all is neutral zone is
calculated by :
Dn
= B /(a
. SR)
It is interesting
also to be able to calculate the neutral
zones for different stereoscopic ratios.
The use of cameras with various lenses,
of binoculars, of field-glass, makes the
stereoscopic ratio in relation to their
magnification factor.
|
|
Nearest subject
Any subject at
a short distance D from the camera will
not be visualize normally if SR is over
its maximum value. It must be cared to evaluate
the distance to the nearest plan and to
determine the desired 3D level.
distance D min
as per L , B and SR
For a known distance
L and a planned base B we can determine
the distance D-min where to set for the
degree of relief chosen by the SR
value..
-
-
The background
being very far
L is great compared
to D and D/(D+L) tends toward 1
Thus D = B / (SR . a ) Now
with the maximum value SR = 50 and a = 0,0004
there is D min = 50 . B which is
the 1/50 rule.
|
CONVERGENCE
of OPTICAL AXIS
In all before, it is
supposed that the two cameras have their optic
axis strictly parallel. The stereoscopic
pairs thus done are perfect for subjects moderately
distant, or in the far. It is true for aerial
photography, for landscapes.
It is quite different
for very near subjects, and when the base is
rather large.
If the last background plan is
not too far from the subject, the convergence will
be benefic. On the other hand, if the last background
plan is very far, the two images of the background
will be shifted, and it will be necessary to mask
the lateral parts not superposed to avoid the visual
trouble when looking at the views. |
|
Beyond 50m our eyes
don't converge any more. On the contrary, more near
is the place we are looking at, the more our eyes
are converging.
In general, each eye can
converge up to 12° and will normally adapt to
a converging angle of 5°. So, as the base is
not greater than 1/5th of the distance to an object,
B>D/5, we should theoretically be able to see
the stereoscopic pairs.
However, it will depends on the
means of visualization. With viewers, it will be
possible. When projecting, it is more difficult. |
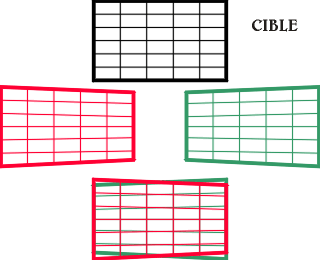
KEYSTONING
EFFECT
The horizontal
and vertical lines are never displayed parallel,
but they run to the infinity end of the
axis lines, upward, or downward as well
as toward the right and the left sides.
It is well known that when turning the camera
upward the vanishing of vertical lines is
more pronounced.
This keystoning
effect bothers in stereophotography because
the images cannot be exactly superimposed.
When the two optical axis run to a near
point, the keystoning is visible. In red
the vanishing when the left camera is turned
to the right, and in green when the right
one is turned to the left.
The bottom figure
shows the difference when superimposed.
|
|
|
CONCERGENCE
RULE
Let us recall
that
the convergence
do not modify the stereoscopic ratio.
The
good rule is that the backgrounds are perfectly
superimposed.
|
|
Thus,
¤ when the
background is very far from the foreground,
the optical axis will be parallel.
¤ when the
background is close to the subject, it is
possible to make converging the optical
axis if assuring that the background is
perfectly superimposed on both views.
|
-
|