PRINCIPES  FONDAMENTAUX  de la STEREOSCOPIE

 

Le contenu de la première partie de cette page jusqu'au paragraphe "rapport stéréoscopique" a été présenté le 5 novembre 2002 à KAPiCA 2002, conférence internationale sur la photographie aérienne avec cerf-volant, et a été mis à jour et complété depuis.

PREAMBULE La clef du succès en photographie stéréoscopique tient à une compréhension et une connaissance claires du processus stéréoscopique et des paramètres qui le contrôlent. Nous savons aussi par expérience que la stéréoscopie paraît plus ou moins forte selon les cas, et nous verrons comment s'en arranger pour des photographies réussies.    Cette page décrit les principes fondamentaux.  Consulter aussi sensation 3D et restitution

CONDITION  pour  la  STEREOSCOPIE La stereoscopie est un processus à la fois physiologique et géométrique. Pour obtenir un effet stéréoscopique, l'image dans notre oeil droit et celle dans notre oeil gauche doivent être similaires, mais avec de légères différences géométriques. Auquel cas, notre cerveau interprète l'image et reconstitue le relief. Si les deux images n'ont aucune différence, l'effet stéréoscopique n'existe pas. De cela découle que la stéréoscopie est effective à la condition suivante:

Les points P1 et P2 doivent être differenciés par nos yeux.     LIMITES  PHYSIOLOGIQUES

Acuité de l'oeil L'acuité est la capacité de l'oeil à distinguer deux points rapprochés. Nous ne pouvons distinguer deux points qui se trouvent dans un angle de moins d'une minute de notre oeil. Mathématiquement, l'acuité est un angle exprimé en radian:  a = 0.0003 à 0.0004

Séparation des couleurs Nous ne pouvons bien distinguer les couleurs que si leur surface est suffisamment grande, et si les zones avoisinantes ont une teinte différente. Cela peut affecter l'effet stéréoscopique par ce que les images gauche et droites peuvent ne pas paraître différentes.

 

 

PARAMETRES de la SCENE

Il faut considérer un paramètre non-géométrique, et deux paramètres géométriques:   Configuration de l'arrière-plan Si l'arrière-plan est d'une même couleur uniforme, il n'y a pas d'effet stéréoscopique.C'est le cas d'un goéland que l'on regarde voler dans un ciel bleu profond uniforme. Notre oeil ne peut différencier les points P1 et P2. Si l'arrière-plan est  varié, avec beaucoup de zones de contrastes et de couleurs différentes, les points P1 et P2 seront réellement différents, et il y aura effet stéréoscopique. La configuration du fond est un paramètre non-géométrique.   Dans une photographie, il n'y a pas un seul premier plan et un seul arrière plan, mais une succession de plans, l'un d'eux pouvant être le plan avant du suivant, et le plan arrière du plan précédent. Les formules pourront se calculer pour chaque couple de plans successifs en fonction de leur disposition réelle.

Distance entre l'appareil et le sujet Ce paramètre intervient pour que l'angle entre les lignes L1 et L2 soit supérieur à la limite de l'acuité. Quand D augmente, l'angle diminue.   Distance entre le sujet et l'arrière-plan Plus l'arrière-plan est éloigné derrière le sujet, et plus les points P1 et P2 seront distants l'un de l'autre. A l'inverse, cela signifie qu'il existe une zone où l'effet stéréoscopique est inexistant car les points P1 et P2 trop proches l'un de l'autre ne peuvent être différenciés. Cette zone est dénommée zone neutre.

PARAMETRES de L' OBSERVATEUR L'observateur peut utiliser ses yeux, mais aussi des jumelles, des systèmes à miroirs, des appareils photo, etc...Tous sont optiquement différents, et vont affecter l'effet stéréoscopique. Appliqué à la photographie, l'appareil photographique constitué de l'objectif et du système imageur, et le dispositif de restitution de l'image peuvent altérer le rendu stéréoscopique.

La Base Pour nous, la base est la distance entre nos yeux, dont la valeur usuelle est 63mm. Utilisant des appareils photographiques, la base peut être modifiée, et c'est le seul paramètre que nous pouvons modifier pour gérer l'effet stéréoscopique. Plus la base est grande, plus l'effet sera marqué.

L'orthostéreoscopie est celle où la base est égale à l'écartement des yeux.

Considérons les distances B, D, L, et l'acuité a, quand la condition pour la stéréoscopie est appliquée, nous avons deux relations simples:               e/(D+L) > a   et   B/D  =  e/L

De celles-ci, les formules en découlent facilement:         Zone neutre  N = a . D² / (B - a . D)         Base                    B >  a . D (D+L) / L

La formule pour la base donne la base minimum à utiliser. Comme nous l'avons dit, la sensation de stéréoscopie peut être forte ou faible. Aussi, il est intéressant pour nous d'apprécier et de quantifier cette sensation stéréoscopique, au moins à partir des paramètres géométriques. Pour ceci, nous allons utiliser le rapport stéréoscopique SR. Je dois admettre que je ne connais pas de règle ou de formule universelle unanimement reconnue pour ce but. Pendant des années, j'ai appliqué la formule du pouvoir stéréoscopique, reprise d'un livre, que j'ai publiée dans un article de Aerial Eye,de l'été 1998 Mais j'ai observé qu'elle ne fonctionnait pas correctement dans quelques cas, même si c'était satisfaisant la plupart des cas. Après quelques recherches infructueuses dans un petit nombre de publications, je m'y suis mis moi-même, reconsidérais l'ensemble, exprimant une nouvelle argumentation, et établissant une formule polyvalente. Note: Les formules sont établies pour un angle de champ identique à la vision stéréoscopique humaine qui n'excède pas 60°

La distance minimum entre deux points que notre oeil peut discerner sur l'arrière-plan est s, et la distance entre les deux points projetés du sujet sur l'arrière plan est e. Comparons-les!   Le rapport stéréoscopique est SR  =  e / s         Si e = s le rapport stéréoscopique est égal à 1 Avec e = BL/D et s = a (D+L)  on obtient:   SR = B . L / a . D . (D+L)   Des tableaux peuvent être calculés.  Pour l'oeil:         0 < SR <  1   effet de relief  nul.         1 < SR < 10  effet de relief  faible.       10 < SR < 20  effet de relief  modéré.       20 < SR < 35  effet de relief  renforcé       35 < SR < 50  effet de relief  fort       50 < SR  < 70  effet de relief excessif                au delà  la stéréoscopie est dérangeante ou impossible.

 

LIMITES  de  L'EFFET  STEREOSCOPIQUE

CONVERGENCE  des  AXES OPTIQUES

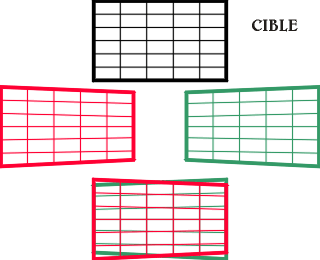
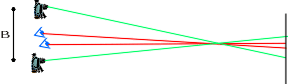
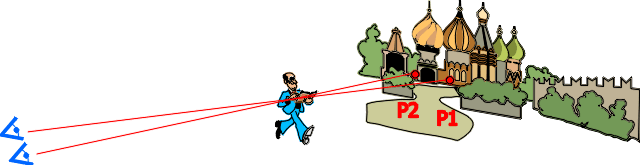
Dans tout ce qui précède, il est supposé que les deux appareils ont leurs axes optiques rigoureusement parallèles. Les paires d'images stéréoscopiques ainsi formées sont parfaites pour des sujets moyennement éloignés ou lointains. C'est vrai pour la photographie aérienne, pour les paysages.  Il n'en va pas de même pour les sujets très proches, et une base relativement large. Si le dernier plan n'est pas trop éloigné du sujet, la convergence sera bénéfique. 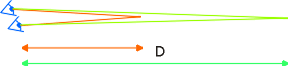Par contre, si le dernier plan en est très éloigné, les deux images de l'arrière plan seront décalées, et il faudra masquer les parties latérales non superposées pour éviter de troubler la visualisation des vues.

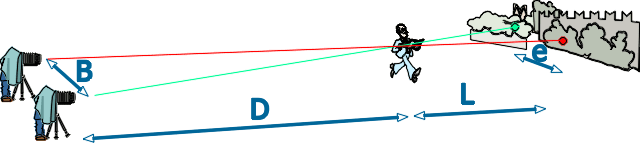
Au delà de 50m, nos yeux ne convergent plus. A l'inverse, plus l'objet que nous regardons est proche, plus nos yeux convergent. En général, chaque oeil peut converger jusqu'à 12° et s'adaptera normalement à une convergence de 5°. Ainsi, tant que la base ne dépasse pas le cinquième de la distance à un objet, B<D/5, nous devrions théoriquement pouvoir visualiser les paires stéréoscopiques. Cependant, tout dépendra du moyen de visualisation. Avec des viseurs, ce sera possible. En projection, c'est plus difficile.

 

CONVERGENCE  des  PERSPECTIVES

Les lignes horizontales et verticales ne sont jamais reproduites parallèles, mais elles fuient vers les points d'axe situés à l'infini, tant vers le haut, ou vers le bas que vers la droite, ou vers la gauche. Il est bien connu qu'en tournant l'appareil vers le haut, la fuite des lignes verticales est accentuée. Cette fuite est gênante pour la stéréophotographie car les images ne sont alors plus exactement superposables. Lorsque les axes optiques sont dirigés vers un point rapproché, l'effet de fuite des perspectives est accentué. En rouge la fuite quand l'appareil de gauche est tourné vers la droite, et en vert quand l'appareil de droite est tourné vers la gauche. La figure en bas montre la superposition qui ne coïncide pas.

 

REGLE  de  CONCERGENCE

Rappelons que la convergence ne modifie en rien le pouvoir stéréoscopique. La bonne règle est que les derniers plans soient parfaitement superposés. Ainsi lorsque l'arrière plan est très éloigné des premiers plans, les axes optiques seront parallèles. Lorsque l'arrière plan est proche du sujet principal, il est possible de faire converger les axes optiques en s'assurant que l'arrière plan se superpose parfaitement sur les deux vues.

 

Copyright becot.info