La convergence est l'angle q formé par les axes optiques des deux lentilles. Les lentilles sont nos yeux, les objectifs, les stéréoscopes, etc. Cet angle est exprimé en degrés.

Lorsque les axes sont parallèles, la convergence est  q = 0.

Les formules de la convergence sont:

 

Voici les valeurs de q avec un écart interoculaire de 65 mm en fonction de la distance D du centre de convergence.

Doubler la base revient à doubler D en conservant le même angle de convergence.

 

Il peut y avoir convergence à la prise de vue; il peut aussi y avoir convergence ou divergence à la restitution lorsqu'il s'agit de deux projecteurs sachant que les phénomènes optiques sont les mêmes à la prise de vue et à la restitution.  C'est généralement un problème quand le calage des projecteurs n'est pas fait correctement et que les disparités de points homologues des images dépassent la distance interoculaire.

 

Dans ces paragraphes, c'est la convergence à la prise de vue souvent ignorée, parfois rejetée, qui est examinée.

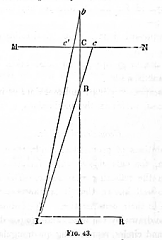
En 1856 Sir David Brewster dans le chapitre VIII de l'ouvrage The stereoscope a le premier indiqué les conditions de stéréophotographie (voir texte et figure ci-contre).

Ainsi, dans le cas de portraits, à une distance de 6 pieds, soit 180 cm, la convergence ne doit pas dépasser 2°. Le calcul confirme qu'avec 2° à 180 cm la base est de 63 mm. Le pouvoir stéréoscopique SR est calculé pour un second plan ou une profondeur d'objet L derrière le premier plan .L'effet va de normal à fort et est excessif pour L > 2,4m (4,2 m de l'objectif)

On ne peut que remarquer l'extrême justesse de la préconisation de Sir D. Brewster, car dans le cas considéré, l'arrière plan est peu éloigné, 1 à 3 m, et pas à l'infini.

En 1895 dans La stéréoscopie de précision, Louis Cazès examinait la convergence. Le plan d'horizon et le plan vertical médian sont reconstitués et homologues. Les autres points sont reconstitués par lignes verticales mais subissent une déformation dans le sens horizontal, toutefois les points homologues restent très voisins de la coïncidence.

 

.Quelques appareils stéréoscopiques sont construits avec les objectifs convergents. C'est le cas du Fujifilm W1

Finalement, la pertinence de la convergence repose sur la tolérance de perception de l'oeil qui est le cercle de confusion. 

Les premiers appareils stéréoscopiques binoculaires avec les deux vues sur la même plaque ne permettaient pas la convergence des vues.

En 1923 le Traité général de stéréoscopie d'Emmanuel Collardeau décrivait un dispositif de convergence pour les vues stéréoscopiques de petits objets. Il précise que ces vues sont parfaitement reconstituées par l'oeil. Dans le même ouvrage il décrit la convergence de vues aériennes verticales en avion.

En 1990 Serge Gauthier publie Traité et méthodes modernes de stéréoscopie qui est une étude détaillée de la convergence. Il  l'explique sur des figures géométriques très bien dessinées. Il produit la méthodologie déterminant la convergence à appliquer pour chaque distance du premier plan.

 

La convergence rapproche les plans vers l'avant. Si le sujet est proche et l'arrière plan indistinct du fait de la mise au point, la convergence sur ce sujet le place dans le plan de la fenêtre  et le mettra en valeur.

Avec la convergence, en même temps que les plans sont perçus plus vers l'avant, l'objet proche est vu plus petit que le même sans la convergence.

La convergence est aussi le moyen de gérer un jaillissement.

La convergence fait qu'un plan perpendiculaire à l'axe central sestvu avec un contour trapézoïdal dans chaque axe optique des objectifs. C'est l'effet keystone. Le côté droit des images sera plus grand sur l'image droite et moindre sur l'image gauche. Ce sera l'inverse pour le côté gauche. Ce ne sera perceptible que pour les lointains de grands angulaires combinés avec une très forte convergence, ce qui est  vraiment peu probable.

La convergence est finalement recommandée pour les sujets proches à condition de ne pas l'exagérer et de contenir l'effet trapézoïdal et le jaillissement de quelques rares sujets.

Avec des champs angulaires de plus de 50° une convergence de 2° ne sera pas pénalisante pour les lointains, et au contraire améliorera le rendu du premier plan.

Ajuster la convergence est nécessaire pour les sujets très rapprochés et aussi dans l'utilisation de zooms de champ angulaire de moins de 30°.

Si l'arrière plan est peu éloigné des premiers plans, il y aura avantage à augmenter l'angle de convergence pour capter des sujets très proches.

La parallaxe linéaire correspond aux disparités entre les images gauche et droite. Elle varie selon la distance D de l'appareil et la profondeur L entre les plans.. Elle a des limites à respecter.

La convergence décale tous les points de l'image un peu comme deux calques superposés déplacés latéralement. Cela revient à retrancher une valeur constante à toutes les disparités.

La parallaxe linéaire peut être modifiée à la restitution en décalant latéralement les images. L'effet est identique à la convergence, mais ce sera au détriment de zones latérales qui devront être rognée. La convergence à la prise de vue conserve la pleine largeur de l'image

Longtemps j'ai scrupuleusement respecté l'exigence de parallélisme habituellement préconisée en réglant avec soin le parallélisme de mes appareils jumelés.

Maintenant j'ai réalisé que la convergence ne modifie pas le ratio stéréoscopique et la profondeur du relief mais améliore le rendu en évitant les violations de fenêtre des plans proches et en préservant le cadrage des images..

 

Les appareils stéréoscopiques bi-objectifs sont parfois construits avec une légère convergence, entre 1 et 2°, le centre de convergence des axes optiques est situé entre 1,8 et 4 m.

 

Beaucoup de films 3D sont tournés avec les caméras en convergence.