- FOREWORD
-
- "How high is the kite"
is an everlasting question. It is common to speak
of the height of a kite, however the exact term is elevation.
- Here I summarizes the main elements
of investigations and developments I started in 1992 to
determine the elevation of a kite.
- The elevation of kite can be a concern
for some scientific experiments, where there are some regulations
on the height of kite, or because of applications such as
kite aerial photography.
|
-
|
-
-
- ALTIMETER
-
- Setting an altimeter on the kite
is an accurate way to measure the elevation of the kite.
Electronic devices are becoming cheaper. The only difficulty
is to send the data to the ground. There are some solutions.
- One similar way can be to have
a GPS device.
|
- TELEMETER
-
- Telemeter is a wonderful device.
If you can walk under the kite, and target it, here is the
height!
- Otherwise, measure the distance
D to the kite and the angle b between kite and horizon, then apply the
formula
- H = D x
sin b
- The accuracy of this method depends
mainly on the measurement of the angle, and ends to ±4%.
- Unfortunately, telemeters for
distances greater than 20m are very expensive. Too bad.
-
|
-
|
-
|
-
- A re-designed protractor is useful for angle measurement.
Difficult to be better than ±2°.
-
|
-
|
- BASIC TRIANGLE
-
- Without any electronic device,
we can estimate the line length. Some kiters, and many kapers
are marking their lines, every 100m and/or every 50m.
-
- With this method, the line is considered
as straight, when in fact, it is curved. So the calculated
height is normally always greater than the true one. In
fact, there is also the elongation of the line under stress:
- Kevlar -> 2%
- dyneema -> 3%
- Polyester -> 10%
- Polyamide -> 20%
- under the maximum stresses.
|
- KITE LINE CURVES
-
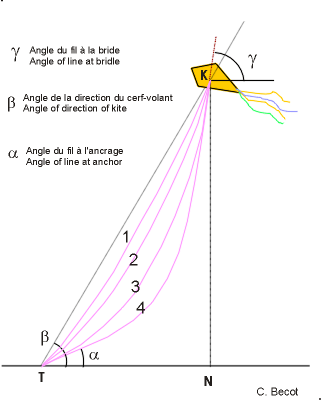
- There are different shapes of
curves of the kite lines. They depends on the kite pull,
the length and size of the line, its weight, the pull of
the wind on the line.
- The mathematical equation of such
curve shall take in account these physical parameters, and
it makes it quite complex.
-
- The figure shows how different
the curves of the line can be.
-
- I have tried to find more simple
way to get an acceptable result. For all of them, the length
of line have to be known, and angles have to be measured.
- I have first considered calculations
based on angles of kite direction, and of kite line.
- Here below are the different methods
I have established.
|
-
|
-
|
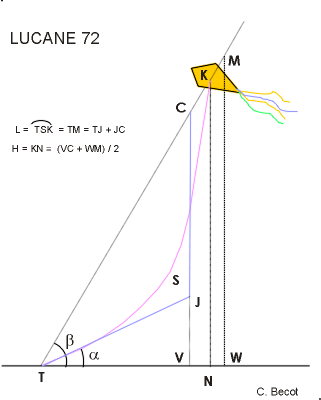
- LUCANE 72 METHOD
-
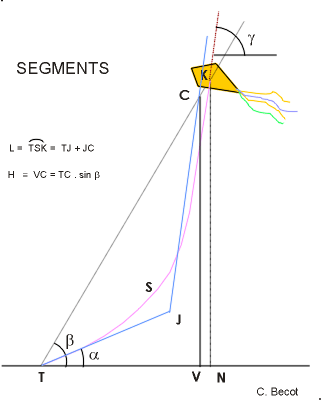
- In the Cerf-Volant Club de France
magazine, Le Lucane N° 72, June 1995, I published a
paper with a formula. I considered the true height NK half
way between the triangle calculation TWM, and between another
VC supposing the line is following two straight lines. These
straight lines are one oblique TJ, as line angle at anchor
point, the second JC is vertical. They are such as their
total length is equal to the line length L.
-
- During the next years, I remarked
that this method is always underestimating the height as
calculated. However, it is often largely compensated by
the material elongation.
-
- This method is also more appropriate
and result more acceptable when there is a load hanging
at J, such as a kap rig.
-
- Anyway, not satisfied enough, I
successively draw two other ways to follow the line curve.
|
|
|
-
|
|
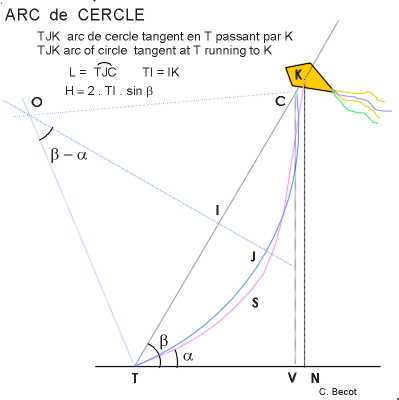
TANGENT
SEGMENTS METHOD
This one is similar to
the Lucane 72 method, but the vertical segment JC is now inclined,
following the line angle at the bridle of the kite. The length
of TJ + JC is equal to the line length TSK.
In theory, the calculated
height VC is always a bit lower than the true one NK. On the
figure, the difference is shown exaggerated for clarity. The
difference is guessed something like 1 to 1,5%. There is much
more uncertainty from angles measures and line length estimation.
To know the line angle
at the bridle, it needs to walk leeward to be able to align
with JK. Or the line angle g
can be measured after take off with
30m line release. It is then necessary to know this angle in
different wind conditions, but experience has shown that it
is then quite predictable. |