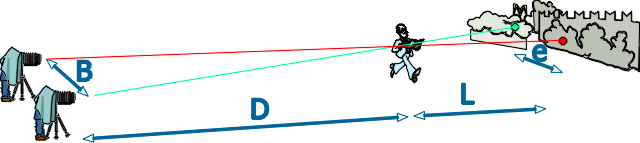
FOREWORD
The page on fundamentals explained
why the stereoscopic effect is greater when the base is
larger. The question is how to calculate the base depending
on the camera and lens which is used.
The human 3D vision is effective
within 60° field. angle. Thus it is common sense to
use as normal lenses giving the same field .
Normally, the horizontal angle
of field of the lens should be taken as the reference. But
the angular field of lenses is often given as the diagonal
field angle.
It is essential to choose
carefully the desired stereoscopic ratio. See the tables
SR / base and distances.
Voir les tableaux SR / base sur
la page correspondante.
1
< SR < 10 weak
10
< SR < 20 moderate
20
< SR < 35 heighten
35
< SR < 50 strong
- NB Hyper-stereoscopy is all relief which is over the
normal visual stereoscopy.
|
|
GENERAL
FORMULA
The fundamental formula to calculate
the base is
B = SR . a
. D (D+L) / L
and is applicable to lenses and
focal lengths giving 60° angle of field.
SR stereoscopic
ratio (see Fundamentals page)
a eye
keenness a = 0.0004
D distance from
camera to subject
L distance
from subject to background
-
CALCUL et
TABLES
Download the xls files
-
|
MANUAL CALCULATION
of the BASE
Base calculation
is rather simple with a programmable calculator, but we
can do it with a simple calculator
For lenses equivalent
to 35-50 mm which angle of field range 55° to 45°,
the factor 2.tan(A/2) below is taken equal to 1
Considering
the formula, when expressing B in mm, D and L in meters,
with k = 0.0004 we have a simplified formula
B mm = SR . 0,4 . D . (1+t)
/ t when t = L/D
Let choose SR = 2.5 which
is a low conventional stereoscopic effect:
this is
B2,5 =
D . (1+t)
/ t
|
|
- Now, the calculation is really simple:
- Calculate t = L/D
- then get (1+t) / t
- and multiply by D
-
- Example:
D = 30m and L = 90m, so t = 3
- B2,5 = D .(1+3)
/ 3 = 30 . 4 / 3 = 40mm
-
For other stereoscopic
ratio, increase the base proportionally.
- To obtain SR
= 5 the base will be double
B5
= 80mm
|
CHANGING
FOCAL LENGH
To the general formula of the base,
it should be added a factor when using different angle of
field. In human vision the horizontal angle is between 50°
and 60°. The reference for lenses will be 60° as
diagonal and 53° as horizontal field angle thus the
field factor is M = 2. tan(53°/2) =1
The factor of a lens with another
field angle is M = 2 . tan (A/2) where A is the horizontal
angle of field of the lens.
B = 2 .
tan(A/2) . SR . a . D (D+L) / L
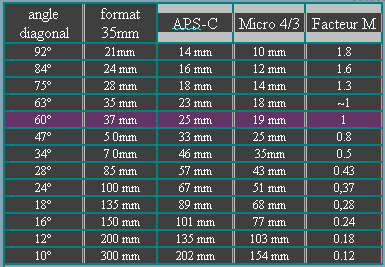
Note:
The diagonal field angle is the
same whatever are the sensors APS-C, 4/3, and the format
of the pictures, 3/2, 4/3, etc.
M varies around de 20% between
50° and 70°. Within this range apply M-=1 will not
really change the stereoscopic ratio.
- Note M = 2 . tan (A/2) =
37 / F* as with 35mm film
|
|
Hereunder are
M factors for common angles of field:
-
|
MACROGRAPHY
In macrography, the magnifying factor
G is to be added:
G = T / F with T extension and F focal
length
B = SR . a
. D (D+L) / L / G
|
|
VIEWING
SYSTEMS
- The stereoscopic effect varies with the viewing system
considering the image is viewed at the standard distance,
or not, because it modifies the magnification of the picture.
- The factor to apply is cos 30° . Dp / Do where
- Dp is the diagonal of the picture
- Dy is the distance of the observer's eye to the
picture.
- The formula is:
SRy = SR
. cos 30° . Dp / Dy
cos 30° = 0.87
|